The development and understanding of new materials play a key role for major industrial and societal challenges of the 21st century. Over the past years more and more materials have been design fully in silico. At the core of this are automated workflows, which systematically perform calculations on thousands to million of compounds. Compared to the early years of materials modelling, which was centred around performing a small number of computations on hand-picked systems, such high-throughput screening approaches have much stronger requirements with respect to the robustness of employed algorithms: even a small percentage of erroneous or failing calculations equals a large number of cases, which need to be checked by a human (causing idle time) and redone thereafter (causing a noteworthy computational overhead).
In my research I want to overcome these obstacles and accelerate computational materials discovery by providing more reliable materials simulations featuring robust error control and built-in uncertainty quantification. Achieving these aspects will not only contribute crucially to reducing the human time required to setup and verify calculations (the typical bottleneck in high-throughput workflows), but it will also enable promising prospects such as active learning or adaptive numerical schemes, which automatically balance errors in order to obtain a simulation result along a path of least computational effort.
This work is inherently a multidisciplinary research effort and in my work I frequently collaborate across domain boundaries. A central component of my efforts is therefore to develop interdisciplinary software platforms which allow all involved communities to synergically join their forces. Building on top of my codes I explore emerging opportunities such as mixed-precision linear algebra or algorithmic differentiaton for materials modelling and investigate their perspectives to obtain more efficient simulations or to better integrate physical models with data-driven approaches.
My collaborations span across the disciplines and include application scientists, mathematicians and computer scientists alike. Recently I have joint multiple interdisciplinary research initiatives in which I take a mediating role between the involved communities, for example by providing interdisciplinary software platforms, such as the Density-Functional ToolKit (DFTK), in which our …
read more
Working side-by-side with mathematicians and application scientists (see also collaborations) on a daily basis has allowed me to learn how to mediate and lower barriers between the disciplines. Apart from problems in the terminologies used in the individual subjects a frequent issue is the lack of software, which allows multiple …
read more
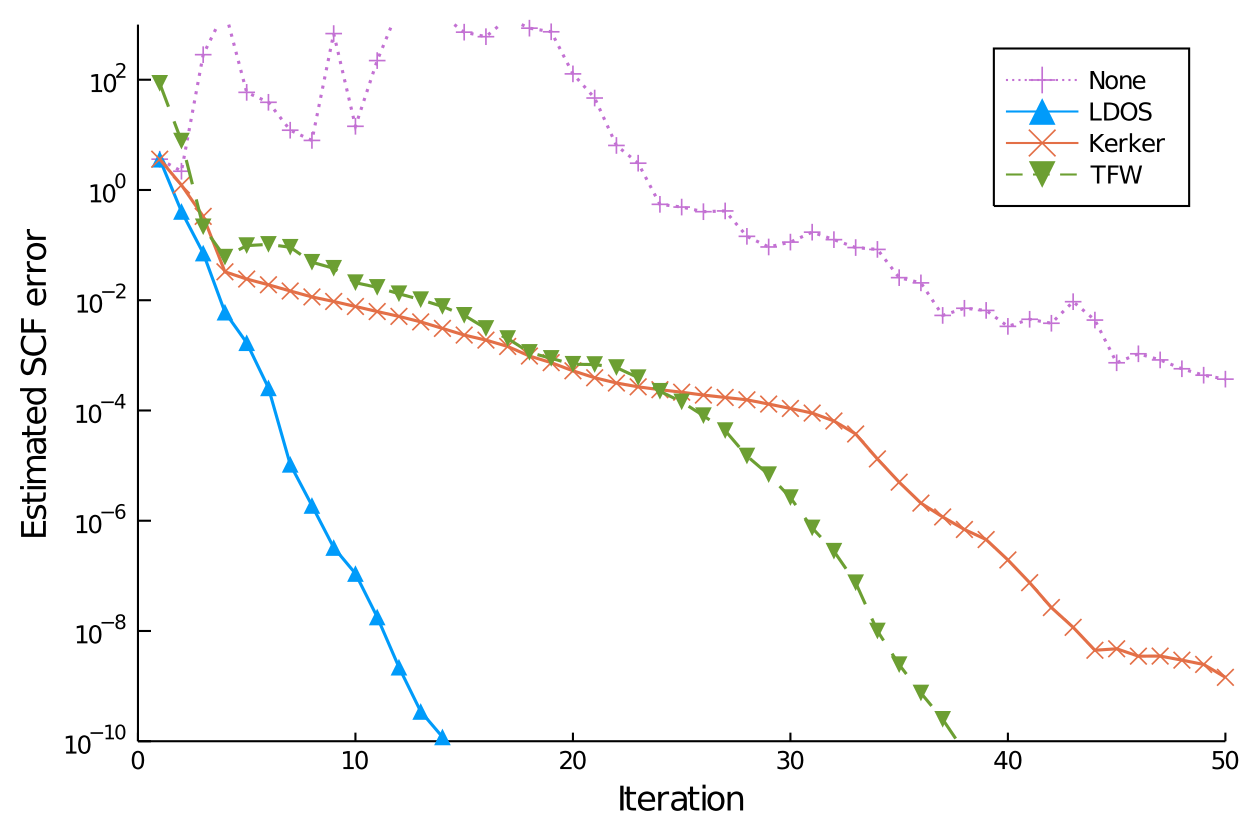
In state-of-the-art DFT algorithms a sizeable number of computational parameters, such as damping, mixing/preconditioning strategy or acceleration methods, need to be chosen. This is usually done empirically, which bears the risk to choose parameters too conservatively leading to sub-optimal performance or too optimistically leading to limited reliability for challenging …
read more
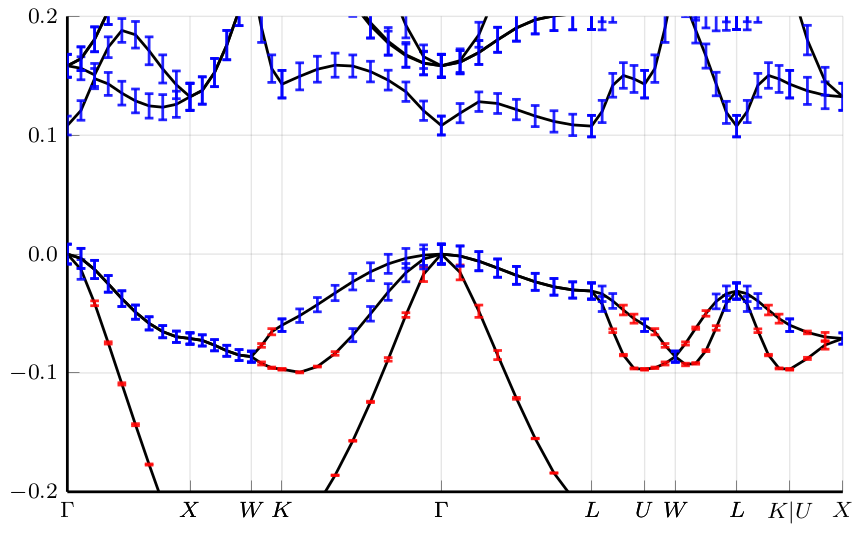
Due to the involved multi-scale nature of standard materials simulation workflows rigorous techniques for error estimates or uncertainty quantification (UQ) are underdeveloped and error analysis on simulation results is rarely attempted. However, recent activities to equip data-driven interatomic potentials with built-in uncertainty measures as well as recent progress on a …
read more
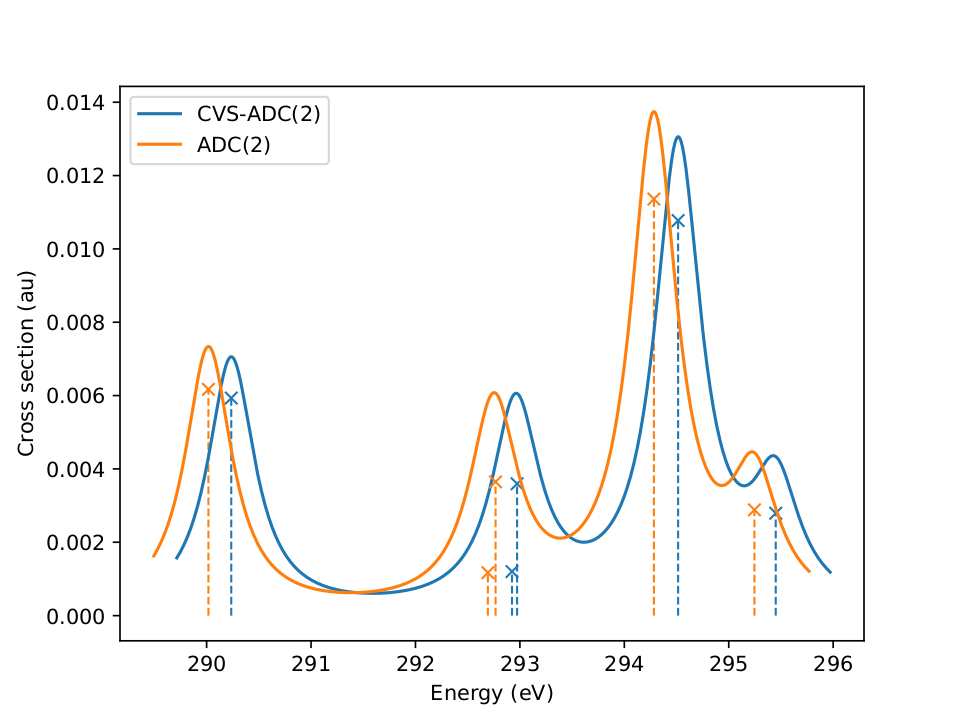
Recently spectroscopic methods in the X-ray regime for the study of the electronic and atomic structure of molecules, have seen key experimental advances. Modelling the involved core-excitation processes accurately is, however, rather demanding. One of the reasons is that the core-excited eigenstates are usually encountered in the same energy range …
read moreIn the first half of my PhD studies in the Dreuw group in Heidelberg I investigated novel approaches for solving the Hartree-Fock (HF) problem using the finite-element method (FEM). The FEM is a standard approach for solving partial differential equations and the aim of the project was to apply it …
read moreIn the second half of my PhD studies I turned my focus towards developing quantum-chemical simulation methods using Coulomb-Sturmian basis functions. Coulomb Sturmians are atom-centred, exponentially decaying functions, which show some desirable properties. For example they are complete and computing the required two-electron integrals is simpler compared to Slater-type orbitals …
read more