Reliable and efficient black-box density-functional theory algorithms
In state-of-the-art DFT algorithms a sizeable number of computational parameters, such as damping, mixing/preconditioning strategy or acceleration methods, need to be chosen. This is usually done empirically, which bears the risk to choose parameters too conservatively leading to sub-optimal performance or too optimistically leading to limited reliability for challenging systems.
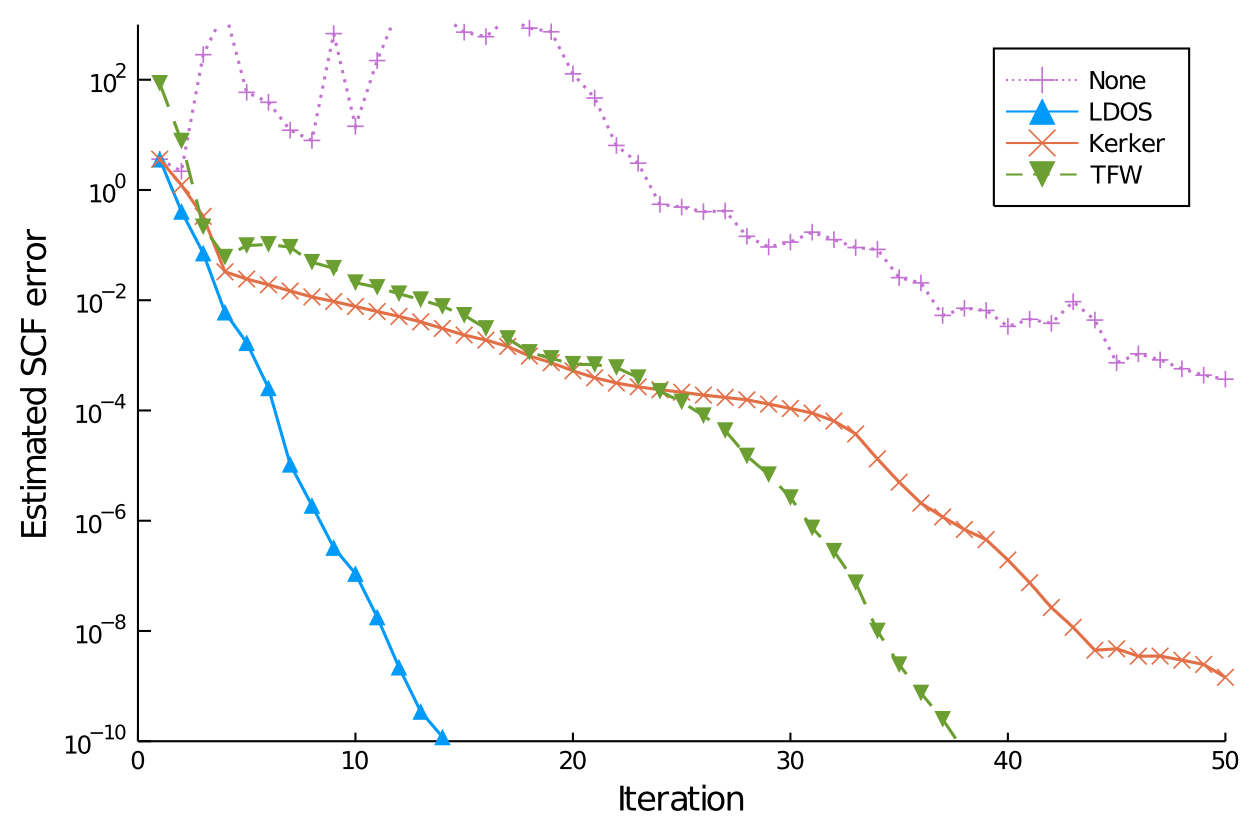
In collaboration with Antoine Levitt (Inria Paris) we recently combined insights from numerical analysis as well as physical principles to suggest both a black-box preconditioner for inhomogeneous materials (see also the figure below). In a second publication we developed an adaptive damping scheme, which improved SCF robustness for a large scope of materials without requiring any manual parameter selection.
  |
||
| Convergence of a selection of self-consistent field methods for an elongated lattice of aluminium (grey) and silica (red/yellow), shown at the top. The LDOS mixing scheme we recently proposed (shown in blue) is able to locally adapt to the material (metal or insulator) and as a result shows a much faster convergence compared to the other approaches. At the same time it is completely parameter-free. |
Unlock efficiency boosts from mixed-precision and randomised methods
In multiple collaboration with researchers from MIT, CMU, Inria Paris and others I currently work on applying and extending these methods furthers. For example one question to consider is numerical stability of DFT algorithms under inexact computations. Even though standard iterative procedures (e.g. Hamiltonian diagonalisation) are usually stopped early to save computational effort, the effect of such numerical noise on the convergence of DFT algorithms has been largely neglected in the numerical analysis to date. Recently a number of opportunities to improve the efficiency of large-scale computations have emerged, which introduce further inexactness in order to increase performance. Examples are mixed-precision methods to exploit low-precision 16-bit floating-point types on modern GPU architectures as well as randomised methods to avoid communication in high-performance calculations. However, to safely exploit such opportunities in the DFT context, understanding and reducing the susceptibility of DFT algorithms to numerical noise is key and thus needs to be investigated more closely.
Highlighted publications
- Michael F. Herbst and Antoine Levitt. A robust and efficient line search for self-consistent field iterations. Journal of Computational Physics, 459, 111127 (2022). DOI 10.1016/j.jcp.2022.111127 [code] Blog article.
- Michael F. Herbst and Antoine Levitt. Black-box inhomogeneous preconditioning for self-consistent field iterations in density-functional theory. Journal of Physics: Condensed Matter, 33, 085503 (2021). DOI 10.1088/1361-648X/abcbdb [code] Blog article.
