Robust error control and algorithmic differentiation in first-principle simulations
Due to the involved multi-scale nature of standard materials simulation workflows rigorous techniques for error estimates or uncertainty quantification (UQ) are underdeveloped and error analysis on simulation results is rarely attempted. However, recent activities to equip data-driven interatomic potentials with built-in uncertainty measures as well as recent progress on a posteriori error bounds for Kohn-Sham problems (e.g. on predicted band structures) offer hope to achieve an error propagation all the way from the DFT level to physical observables of long-running MD trajectories.
In ongoing projects I am involved in the development of both analytical as well as statistical error estimates for materials simulations. This work I underdo in collaboration with experts in numerical analysis as well as uncertainty quantification and as a part of multidisciplinary research efforts such as the MIT Center for Exascale Simulation of Material Interfaces in Extreme Environments or the ERC Synergy Extreme-scale Mathematically-based Computational Chemistry project.
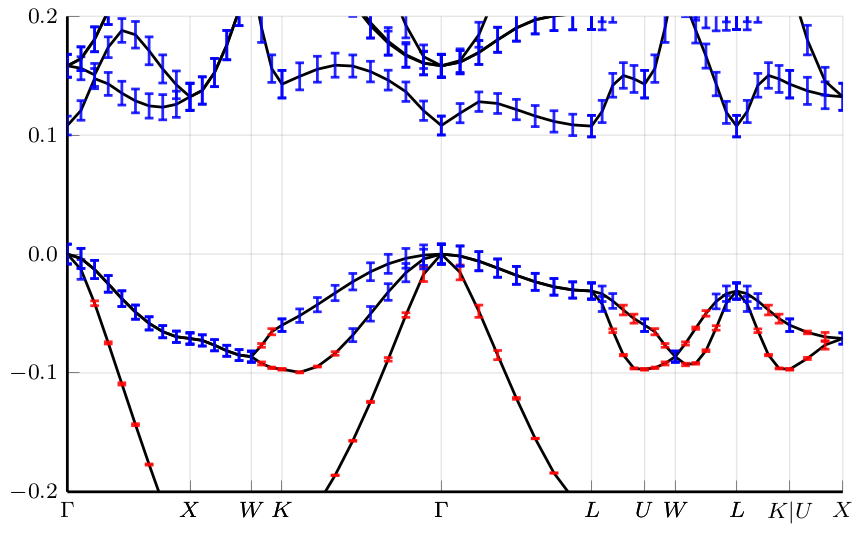 |
||
| Band structure of silicon in a reduced (linear) Kohn-Sham model annotated with guaranteed error bars indicating the total numerical error (due to discretisation/finite basis size, early stopping of iterative procedures as well as finite floating-point arithmetic). More details. |
Algorithmic differentiation
An ongoing effort to support my research on error analysis and uncertainty quantification is to develop a software stack for first-principles simulations, which is fully algorithmically differentiable (AD-able). To achieve this I collaborate both with researchers from the AD as well as the Julia community, e.g. to integrate Julia-based frameworks for AD into our DFTK code (see software).
This framework will allow to automatically compute arbitrary derivatives of macroscopic MD quantities versus any input parameter, such as the parameters of the interatomic potential or the underlying DFT functional. Since the aim is to integrate both with DFT as well as MD methods, this framework will enable e.g.
- a routine computation of the sensitivities of DFT energies/forces wrt. the DFT functional or the employed pseudopotential,
- goal-oriented sensitivity analysis on the predictions of MD trajectories,
- invasive uncertainty quantification approaches across the full DFT/MD pipeline, and
- the ability to backpropagate losses of the DFT energies/forces versus reference results from higher-level first-principle simulations.
In particular (1) and (4) combined will allow to construct data-driven functionals for DFT in the spirit of a physics-informed neural networks, which could allow to obtain a better accuracy per cost ratio than present DFT methods.
Highlighted publications
- Eric Cancès, Michael F. Herbst, Gaspard Kemlin, Antoine Levitt and Benjamin Stamm. Numerical stability and efficiency of response property calculations in density functional theory. Letters in Mathematical Physics, 113, 21 (2023). DOI 10.1007/s11005-023-01645-3 [code] Blog article.
- Michael F. Herbst, Antoine Levitt and Eric Cancès. A posteriori error estimation for the non-self-consistent Kohn-Sham equations. Faraday Discussions, 224, 227 (2020). DOI 10.1039/D0FD00048E [code] Blog article.
